
この記事では、Expert Advisor 戦略を設計し、EA 設定を最適化して最適な長さ、パターン、使用法を決定する方法を学ぶことができます。
前の記事では、すべての外部変数とほとんどの内部パラメータを意図的に分離して、20 ~ 200 の二重単純移動平均 (SMA) クロスオーバー EA を作成しました。は 41 年間 (1971 年 1 月から 2012 年 1 月まで) 信頼されており、2500 ポイント未満の損失で 15000 ポイントを達成するなど、好調な成績を収めました。 私はこの EA が非常にうまく機能すると信じています。その理由は、EA が純粋で (つまり、追加のインジケーター、出口、フィルターによって妨げられていない)、最も一般的な長さとメソッドを借用しているからです。 この記事では、元の EA が異なる長さまたはアプローチからメリットを得られるかどうかを検討します。
高速長には 20 SMA の初期長を選択し、低速長には 200 SMA を選択するのはなぜですか? 複数の場所で読んだように、20 日 SMA が 200 日 SMA を超える場合はゴールデン クロスと呼ばれ、交差する場合はデス クロスと呼ばれます。 これらの用語は、株や先物の世界でより一般的に使用されます。 それらに付けられた造語(金と死)は、その重要性を示しています。長期トレンドを捉える能力により、すべてのプロのトレーダーがそれらをフォローし、主導しています。 中期間のクロスオーバーのインスタンスをより多く生成するために (つまり、より多くの取引を) 生成するために、単純に時間枠を日足バーから H4 バーに変更しました。 このような長い日足で計算された移動平均では、信頼できる統計的評価を行うには取引が少なすぎます。
MACross に何らかの形式の正規化された値を選択すると便利ですが、ゴールデン クロスにはより高い値が機能するようです。 ただし、50 の速い長さから 300 の遅い長さまですべてをテストして、より有利な長さを発見できるかどうかを確認できれば興味深いでしょう。 私は、高速な長さに合わせて最適化することはあまり好きではありません。 最適化には 1 つの長さで十分ですが、より多くの長さまたはパラメーターを最適化すると、過剰な最適化やカーブ フィッティングの危険があります。 いずれにせよ、遅い方が長さが重要です。 代わりに、速い長さを遅い長さの固定比率として保持します。 最初に選択される分数は 1/10 になります。 ファスト 20 がスロー 200 で動作する場合、ファストの長さがスローの長さの 1/10 であれば、ファストの長さは問題なく動作します。 比較的高速な 5 ~ 50 のダブル MA クロスから、比較的遅い (そしてスムーズな) 30 ~ 300 のダブル MA クロスまで、幅広い操作で MACross の機敏性と精度をテストすることは興味深いでしょう。 20-200 ゴールデンクロス自体のパフォーマンスを上回るのは難しいですが、試してみます。
高速移動平均を低速移動平均の固定比率 (1/10) にするにはどうすればよいですか? 1 つは、高速移動平均を外部変数として削除し、分数として表示するだけです:
//外部変数部分に配置します
extern int MAFraction = 10;//Start() 関数の後に配置します
Double MAFastLen = MASlowLen / MAFraction;
最適化について一言。 過剰な最適化の危険性を事前に知り、それを回避するための措置を講じることが正しく行われている限り、ある価値を別の価値と交換するより客観的で、おそらくより収益性の高い理由を提供できます。 過剰な最適化を避けるための手順に関する記事をお読みください。
この最適化実験の目的は、Double MA Crossover EA に使用する最適な長さと方法を決定することです。
2 つの質問をします:
最も遅い移動平均 最適なものは何か長さ?
最適なモード (SMA または EMA) はどれですか?
SlowMA 長の最適化範囲は 50 ~ 300 (10 ステップ) で、25 通りの組み合わせが可能です。 この最適化には単純な移動平均を使用し、次に指数移動平均に対しても同じ最適化を実行します。
1999 年 1 月から 2009 年 1 月までの 10 年間のサンプル期間にわたって長さを最適化します。その期間に最適な長さを選択し、それを使用します。過去 3 年間 (2009 年 1 月から 2012 年 1 月まで) のバックテストで長さを分析し、10 年間の最適化後に取引した場合に選択した長さがどのように機能するかを確認します。
テストアカウントのサイズは 10,000 ドル、ロットサイズは 0.1、ストップロスは 150 ピップスだったので、最大損失トレードは 150 ドル、または 1.5% でした。アカウントのサイズ。
第 1 ラウンド (SMA パターン)
単純移動平均 (SMA) を使用すると、関連する期間のすべての価格が次のようになります。
同等。 SMA は、一定期間にわたる過去の終値の合計を単純に計算し、その結果を計算に使用される価格の数で割ります。
SMA = SUM(Close, N)/N
ここで:
N — 計算数値です。サイクルの。
最適化 #1: 低速の長さを 50 から 300 に最適化し、高速の長さは 20 に保ちます。 最適化には遅い長さが最適です。
以下は、1973 年 2 月から 2013 年 2 月まで (40 年間) のコントロール ポイントを使用してモデル化された二重 SMA 交差点の MASlowLen です:
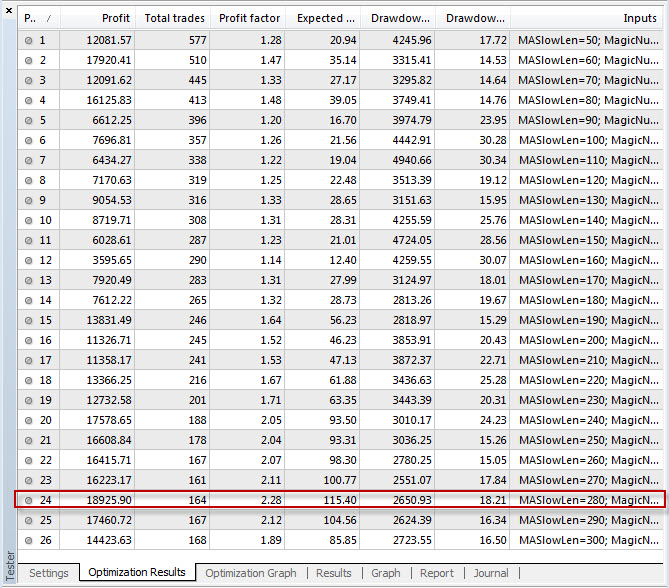
連続する長さが長くなるごとに結果がどのように改善されるかに注目してください。 H4 移動平均クロスオーバーは、より長い長さの平滑化係数で最もよく機能するようです。 絶対的な最高の結果は 280 の遅い長さで、結果として優れた $18925/18925 ピップスと 2.28 という非常に健全な利益率をもたらしました。 200 スローラインよりも 7000 ピップス多く獲得し、最大ドローダウンが 1200 ピップス少ないことに注目してください。 20-200の組み合わせの最大リトレースメントは3853ポイントですが、20-280の組み合わせの最大リトレースメントは2650ポイントです。 それはすべて非常に有望です。
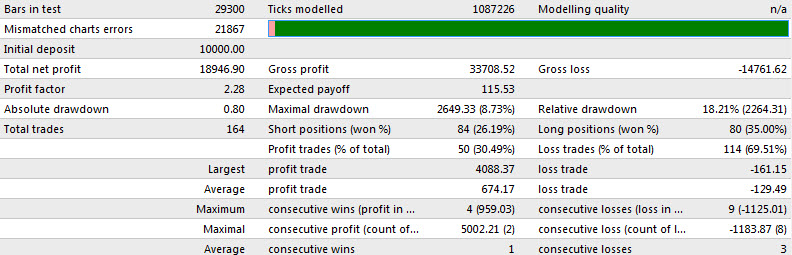
以下で検討する EMA のバージョンは、深刻な競争に直面するでしょう。
ラウンド 2 ( EMA)モード)
指数平滑移動平均は、現在の終値の移動平均の一部を前の値に加算することによって計算されます。 指数関数的に平滑化された移動平均により、最新の価格の価値が高くなります。 利点は、単純な移動平均よりも早くトレンドやトレンドの反転を捉えることができることです。
EMA = (Close(i)*P)+(EMA(i-1)*(1-P))
ここで:
CLOSE(i) — 現在の期間が終了する価格、
EMA(i-1) —前期間の終値 ;
P の指数移動平均 - 価格値のパーセンテージを使用します。
EMA の欠点は、スピードの代わりに滑らかさが犠牲になり、不安定な横ばい市場での誤った取引が増えることです。 短い遅い SMA は長い SMA よりも悪い結果を生み出すことに気づいたので、EMA は同じ速度の問題を抱えているため、SMA ほど成功しないだろうとすでに予測できます。 速度と流暢さの勝負では、速度が最も重要であるようです。
以下は、ダブル EMA クロスを使用した EMASlowLen の最初の 26 件の最適化結果です。
1973 年 2 月から 2013 年 2 月まで (40 年間):
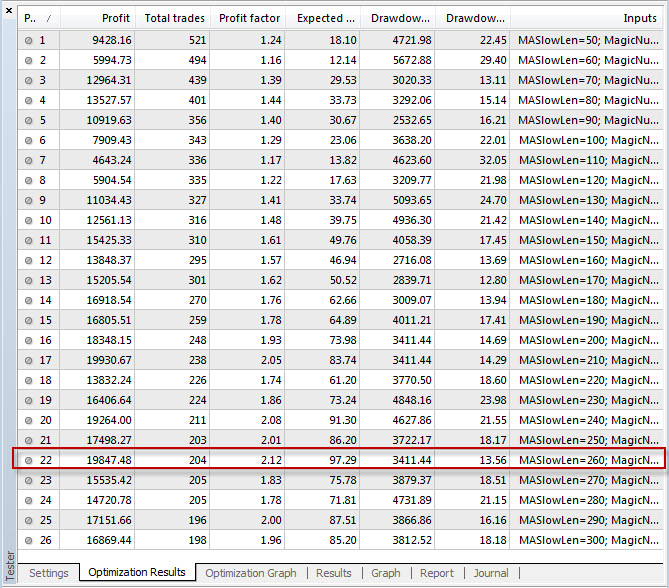
この EMA パターンは、SMA パターンと似ていますが、より収益性の高い結果をもたらします。 最も最適化された 260-EMACros の重みは $19847/19847 ポイントで、280-SMACros よりも 1000 ポイント高くなります。 ただし、SMA クロスオーバーのリトレースメントは 800 ピップス減少します。 長さ 260 が長さ 100 ~ 130 のパフォーマンスを 2 倍にすることに注目してください。さらに、長さを長くすると信頼性が向上することがわかります。
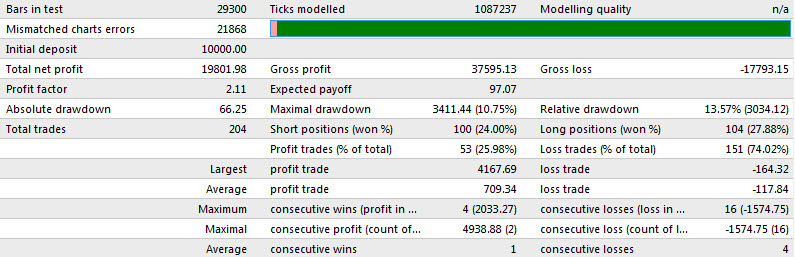
結論
優れた最適化とは、さまざまなパラメータの結果を明らかにして比較し、有望なパラメータを選択し、パフォーマンスの悪いパラメータや過剰最適化のルールに違反するパラメータを削除する発見/削除プロセスです。
手法ごとに異なる長さに沿って二重移動平均クロスオーバー戦略を最適化した場合、長さが長いほど良い結果が得られることがわかりました。 長い長さの方が短い長さよりも速度の点で有利な平滑化効果が得られるようです。 MA が遅いほど、より大きなトレンドを特定してサポートしようとしますが、速い MA 長期化するほど、反転を期待して支配的なトレンドに出入りする意欲が薄れます。 その結果、騒音と鞭のこぎりが減少します。 長さが短いと、最近の動きに敏感になる可能性がありますが、不安定性も高くなります。
単純と指数関数の間で実際に選択してさまざまな方法を比較すると、指数関数のリトレースメントが強い一方で、単純な結果の方が何らかの形で優れていることがわかります。 。 20-280 SMACross は損失を 800 pips 削減するため、最も効果的であることが証明されていますが、20-260 EMACross は 1000 pips 以上の利益を生み出す有力な候補です。 長い長さの滑らかさが短い長さの速度よりも優れているのと同様に、単純な方法の滑らかさ係数は指数関数的な方法の速度係数よりも優れているように見えます。 この指数は、最新の価格ポイントをより重視することで、単純な遅さの要因に対処しようとしています。そうすることで、より早くトレンドや反転に入ることができますが、同時に、市場が不安定な横ばいのせいで、より誤った取引に飛び込む可能性があります。 このような誤ったエグジットは、特に横ばいの市場において、損失取引の数を増加させ、全体的なパフォーマンスを弱める可能性があります。


